#edu2012. 换根DP

换根DP

换根DP

树形DP中换根问题又被称为二次扫描，通常不会指定根结点，并且根结点的变化会影响一些值，例如子结点深度和、点权和等。

对于这种问题，如果暴力枚举每一个点作为根，算法复杂度太高，仔细分析，将根节点与其一个子节点转化的过程中，某些值是可以保留的，不要重头开始算，这个过程就是“换根”。 通常进行两次 DFSDFS，第一次 DFSDFS 预处理诸如深度、点权和等信息，第二次 DFSDFS 开始进行换根动态规划。

例1 .P10974 Accumulation Degree

题意简化：给你一颗树，每条边有一个最大容量，根结点可以流出无限的流，叶子结点可以接受无限多的流，其他结点不储存水。

思路点拨：

首先考虑朴素算法：枚举源点 ss，计算以此点为源所能流出的最大流量。 如把 ss 当做树根，整个水系成为有根树，河道的方向也确定了。根节点流向子树，子树与原问题结构相似，此问题就是一个树形 DPDP 。

设 D[x]D[x] 表示以 xx 为根的子树中，把 xx 作为源点，从 xx 出发流向子树的流量最大是多少。

$D[x]=\sum \left\{\begin{matrix} min(D[sonx],edge[x][sonx]),sonx度>1(sonx不是叶子) \\edge[x][sonx],sonx度=1（sonx是叶子） \end{matrix}\right. $

若 ss 为树根，D[s]D[s] 就是从 s 流出的最大流量，也就是整个树的最大流出流量，枚举每一个结点作为根，此时算法复杂度是 O(n2)O(n^2)

优化：用“二次扫描换根法”代替源点的枚举，可以在 O(N)O(N) 的时间内解决整个问题。

总体思路是：选一个点作为根节点（一般是第一次扫描的根），计算出此点作为整个树根的值，从这个点推算出其儿子作为整个树的根的值。

设 F[x]F[x] 表示把 xx 作为整个树的根，流向整个水系，流量最大是多少？ 那么 F[root]=D[root]F[root]=D[root]

也就是现在 F[x]F[x] 已经求出，考虑其子节点 yy，F[y]F[y] 尚未被计算。

F[y]F[y] 包含两部分：

  • 1.从 yy 流向以 yy 为根的子树的流量，已经计算并保存在 D[y]D[y] 中。

  • 2.从 yy 沿着父节点 xx 的河道，进而流向水系中其他部分。

把 xx 作为源点，总流量是 F[x]F[x]，从 xx 流向 yy 的流量为 min(D[y],edge[x][y])min(D[y],edge[x][y]) ,那么从 xx 流向除 yy 以外其他部分的流量就是二者之差 F[x]−min(D[y],edge[x][y])F[x]-min(D[y],edge[x][y]),那么 yy 如果作为源点，yy 流向 xx 的流量就是 min(F[x]−min(D[y],edge[x][y]),edge[x][y])min(F[x]-min(D[y],edge[x][y]),edge[x][y])。当然，xx 如果度为 11，需要特殊判断。

$F[y]=D[y]+\sum \left\{\begin{matrix} min(F[x]-min(D[y],edge[x][y]),edge[x][y]),x度>1(x不是叶子) \\edge[x][y],x度=1 \end{matrix}\right.$

第二次扫描与换根：原根值已经算完，将儿子作为树根，计算此时的值。

参考代码：点击

例2.P3478 [POI2008]STA-Station

思路点拨：

暴力枚举根节点，以某一个点作为树根，d[x]d[x] 表示 xx 点的深度，DFSDFS 整颗树，计算所有结点的 d[x]d[x] ，累加d[x]d[x] ，找到深度和最大值对应的树根。

设 xx 的儿子 yy ，xx 若为整个树的树根，当 yy 变成树根时，整个树节点深度和增加 n−size[y]n-size[y]（ size[y]size[y] 表示以 yy 为根的子树的大小），减少 size[y]size[y] 。

那么第一次 dfsdfs，计算出 d[x]d[x], size[x]size[x] ，设f[x]f[x] 表示以 xx 为整个树根的深度和，第一次 dfsdfs，也可以计算出 f[root]f[root] 。 第二次 dfsdfs，若 xx 的儿子为 yy ，xx 为根，换做yy 做根，f[y]=f[x]−size[y]+n−size[y]=f[x]+n−2∗size[y]f[y]=f[x]-size[y]+n-size[y]=f[x]+n-2*size[y]。

参考代码：点击

例3. CF1187E Tree Painting

题意简化:给定一棵 nn 个点的树，初始全是白点，要求你做 nn 步操作，每一次选定一个与一个黑点相隔一条边的白点，将它染成黑点，然后获得该白点被染色前所在的白色联通块大小的权值。第一次操作可以任意选点。求可获得的最大权值

思路点拨：

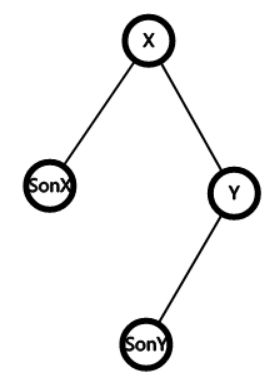
设 f[x]f[x] 表示以 xx 为子树根，子树获取的权值

g[x]g[x] 表示以 xx 为整棵树的根，所能获取的最大值

f[x]=size[x]+∑i∈sonxf[i]f[x]=size[x]+\sum_{i \in sonx}f[i]

以 11 作为树根，g[1]=f[1]g[1]=f[1] ,枚举其他节点求 g[x]g[x],复杂度是 O(n2)O(n^2) , 采用二次扫描换根优化。

即 g[x]g[x] 已经算出，求 g[y]g[y]。

$g[y]=n+\sum f[sony] + n-size[y]+ \sum_{i \in sonx |i \not=y}f[i]$

$=n+(f[y]-size[y])+n-size[y]+\sum_{i\in sonx |i\not= y}f[i]$

=$n+n-2*size[y] + \sum_{i \in sonx |i \not= y}f[i] +f[y] $

=n+n−2∗size[y]+∑i∈sonxf[i]=n+n-2*size[y]+ \sum_{i \in sonx }f[i]

=n+n−2∗size[y]+g[x]−n=n+n-2*size[y]+g[x]-n

=g[x]+n−2∗size[y]=g[x]+n-2*size[y]

vm4DUJ.png

参考代码：点击

P3525 [POI2011]INS-Inspection

luogu题目翻译有问题，题意如下：

一棵 nn 个节点的树，行动中心 SS 从 1−>N1->N 依次选择。

从 SS 出发前往任意一个未标记到的点(沿树上两点的唯一路径走)，标记该节点，然后返回 SS。相邻两次行动所经过的道路不允许有重复，最后一次标记后不需要返回，求路程总和的最小值。

第 ii 行输出行动中心为 ii 时的答案，如果不可能则输出 −1-1

思路分析：

根据题意，如果以 ii 为根，要求相邻两次行动所经过的道路不重复，也就是 ii 的最大子树不能超过 n/2n/2，因为超过以后其他子树点都访问完后，这颗最大子树还有多余 2个节点没有访问，必然出现相邻两次行动走重复道路的情况。

简单证明：如果 nn 个节点的树最大的子树为 yy，其余子树大小之和为 xx,x+y=n−1x+y=n-1,当 y−x>=2y-x>=2 时，无法实现“相邻两次行动所经过的道路不重复”，y>=(n+1)/2y>=(n+1)/2，那么y<=n/2y<=n/2。

也就是说当节点 ii 为重心时，才有解，否则输出 −1-1；

最终答案就是: 2∗∑d[i]−max(d[j])2*\sum d[i]-max(d[j]),d[i]d[i] 表示从根节点到 i 的距离,由于折返，所以乘以 22，最后停在 jj，少走 d[j]d[j] ,当然需要停在距离根节点最远的节点 j上，这样走过距离最小。

不过这里有一个特殊情况，当 nn 为偶数，例如 n=10n=10,有两颗子树，一颗为 55，一颗为 44 ,最后只能停在 55 这颗子树上，但是 55 这颗子树不一定是最远距离，也就是要去 55 这颗子树距离根的最远距离，然后减掉。

参考代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
vector<int>e[N];
int n,dep[N],siz[N],fa[N];
bool core[N];
long long ans;int maxlong;
int d[N];  //d[x] 表示以x为根的子树中距离x最远的距离 
void dfs(int x,int father)
{
	dep[x]=dep[father]+1;
	siz[x]=1;
	fa[x]=father;
	for(int j=0;j<e[x].size();j++)
	{
		int y=e[x][j];
		if(y==father)continue;
		dfs(y,x);
		siz[x]+=siz[y];			
	}
}
bool check(int x)
{
	if(n-siz[x]>n/2)return false;
	for(int i=0;i<e[x].size();i++)
	{
		int y=e[x][i];
		if(y==fa[x])continue;
		if(siz[y]>n/2)return false;		
	}
	return true;
}
void dfs2(int x,int father)
{
	dep[x]=dep[father]+1;
	maxlong=max(maxlong,dep[x]-1);
	ans+=dep[x]-1;
	d[x]=0;
	siz[x]=1;
	for(int i=0;i<e[x].size();i++)
	{
		int y=e[x][i];
		if(y==father)continue;
		dfs2(y,x);
		d[x]=max(d[x],d[y]+1);
		siz[x]+=siz[y];
	}
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<n;i++)
	{
		int a,b;
		scanf("%d%d",&a,&b);
		e[a].push_back(b);
		e[b].push_back(a);
	}	
	dfs(1,0);	
	
	for(int i=1;i<=n;i++)
		if(check(i))
			core[i]=1;
	
	
	for(int i=1;i<=n;i++)
		if(core[i])
		{
			ans=maxlong=0;
			dep[0]=0;
			dfs2(i,0);
			for(int j=0;j<e[i].size();j++)
			{
				int y=e[i][j];
				if(siz[y]==n/2)
				{
					maxlong=d[y]+1;
					break;
				}
			 } 
			printf("%lld\n",ans*2-maxlong);
		}
				
		else
			printf("-1\n");
			
	return 0;
}

P3574 [POI2014] FAR-FarmCraft

题意：

给定一棵 nn 个节点的树，访问每一个节点，给每个节点发一台电脑，节点安装电脑需要 cic_i 的时间，访问完节点，就会离开，节点有人自己安装电脑，最后回到节点 11。询问如何发电脑，使得所有节点安装完电脑所用时间最短。

思路分析：

设 f[x]f[x] 表示以 xx 为根的树，所有节点安装完电脑所用的最短时间。

运送电脑路上所花的时间实际上是固定的，主要是送到后节点还需要安装，还需要等待，关键点就成了如何安排运送顺序使得 f[x]f[x] 最小。

对于一般情况，我们可以得到状态转移方程：

f[x]=max(f[x],siz[x]+1+f[y]f[x]=max(f[x],siz[x]+1+f[y],yy 是 xx 的儿子，其中 siz[x]siz[x] 表示访问 yy 之前所走的时间。含义如下图：

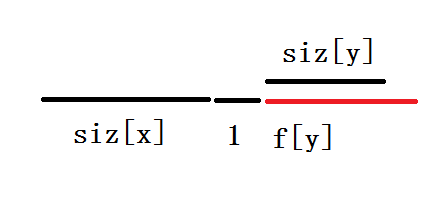
jgfSnP.png

注意：siz[x]siz[x] 表示访问 yy 之前路上花的时间,从 xx 到 yy 花 11 的时间,f[y]f[y] 以 yy 为根的子树完成的最短时间，肯定会比 siz[y]siz[y] 大。

结果与子树遍历顺序有关，可以用微扰法找到排序的关键字。

如果先访问 yy，访问 zz，可以得到

f1[x]=siz[x]+max(1+f[y],2+siz[y]+1+f[z])f_1[x]=siz[x]+max(1+f[y],2+siz[y]+1+f[z])

如果交换，可以得到

f2[x]=siz[x]+max(1+f[z],2+siz[z]+1+f[y])f_2[x]=siz[x]+max(1+f[z],2+siz[z]+1+f[y])

交换前更优，等价于f1[x]<f2[x]f_1[x]<f_2[x]

即$max(1+f[y],2+siz[y]+1+f[z])<max(1+f[z],2+siz[z]+1+f[y])$

max(f[y],2+siz[y]+f[z])<max(f[z],2+siz[z]+f[y])max(f[y],2+siz[y]+f[z])<max(f[z],2+siz[z]+f[y])

由于f[y]<2+siz[z]+f[y],f[z]<2+siz[y]+f[z]f[y]<2+siz[z]+f[y],f[z]<2+siz[y]+f[z]

上式等价于2+siz[y]+f[z]<2+siz[z]+f[y]2+siz[y]+f[z]<2+siz[z]+f[y]

即：f[z]−siz[z]<f[y]−siz[y]f[z]-siz[z]<f[y]-siz[y]

也就是 f[y]−siz[y]f[y]-siz[y] 越大，应该早访问，对于每一个节点 xx,其所有儿子节点 f[y]f[y] 确定后，按照关键值 f[y]−siz[y]f[y]-siz[y] 从大到小排序,从而获得访问顺序。

参考代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10;
int n,c[N];
vector<int>e[N];
int f[N],siz[N];
bool cmp(int y,int z)
{
	return f[y]-siz[y]>f[z]-siz[z];
}
void dfs(int x,int fa)
{
	f[x]=c[x];
	for(int i=0;i<e[x].size();i++)
	{
		int y=e[x][i];
		if(y==fa)continue;
		dfs(y,x);
	}
	sort(e[x].begin(),e[x].end(),cmp);
	for(int i=0;i<e[x].size();i++)
	{
		int y=e[x][i];
		if(y==fa)continue;
		f[x]=max(f[x],siz[x]+f[y]+1);
		siz[x]+=siz[y]+2;
	}
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)scanf("%d",c+i);
	for(int i=1;i<n;i++)
	{
		int a,b;
		scanf("%d%d",&a,&b);
		e[a].push_back(b);
		e[b].push_back(a);
	}
	dfs(1,0);
	int ans=max(f[1],siz[1]+c[1]);
	printf("%d",ans);

	return 0;
}

学习完毕

{{ select(1) }}

  • YES
  • NO
  1. 关于
  2. 联系我们
  3. Language
  4. 兼容模式
  5. 主题
  3. Worker 0 in 63ms
  4. Powered by Hydro v4.19.1 Modified by byx QQ465039728
  5. 陕ICP备2023000766号