#P1837E. Playoff Fixing
Playoff Fixing
Description
$2^k$ teams participate in a playoff tournament. The teams are numbered from $1$ to $2^k$, in order of decreasing strength. So, team $1$ is the strongest one, team $2^k$ is the weakest one. A team with a smaller number always defeats a team with a larger number.
First of all, the teams are arranged in some order during a procedure called seeding. Each team is assigned another unique value from $1$ to $2^k$, called a seed, that represents its starting position in the playoff.
The tournament consists of $2^k - 1$ games. They are held as follows: the teams are split into pairs: team with seed $1$ plays against team with seed $2$, team with seed $3$ plays against team with seed $4$ (exactly in this order), and so on (so, $2^{k-1}$ games are played in that phase). When a team loses a game, it is eliminated.
After that, only $2^{k-1}$ teams remain. If only one team remains, it is declared the champion; otherwise, $2^{k-2}$ games are played: in the first one of them, the winner of the game "seed $1$ vs seed $2$" plays against the winner of the game "seed $3$ vs seed $4$", then the winner of the game "seed $5$ vs seed $6$" plays against the winner of the game "seed $7$ vs seed $8$", and so on. This process repeats until only one team remains.
After the tournament ends, the teams are assigned places according to the tournament phase when they were eliminated. In particular:
- the winner of the tournament gets place $1$;
- the team eliminated in the finals gets place $2$;
- both teams eliminated in the semifinals get place $3$;
- all teams eliminated in the quarterfinals get place $5$;
- all teams eliminated in the 1/8 finals get place $9$, and so on.
Now that we established the rules, we do a little rigging. In particular, we want:
- team $1$ (not team with seed $1$) to take place $1$;
- team $2$ to take place $2$;
- teams $3$ and $4$ to take place $3$;
- teams from $5$ to $8$ to take place $5$, and so on.
For example, this picture describes one of the possible ways the tournament can go with $k = 3$, and the resulting places of the teams:

Some seeds are already reserved for some teams (we are not the only ones rigging the tournament, apparently). We have to fill the rest of the seeds with the remaining teams to achieve the desired placements. How many ways are there to do that? Since that value might be large, print it modulo $998\,244\,353$.
谷歌翻译
球队参加季后赛。这些队伍的编号从 到 ,按照实力递减的顺序排列。所以, 队是最强的, 队是最弱的。数字较小的球队总是会击败数字较大的球队。
首先,在称为种子的过程中,球队按某种顺序排列。每支球队都会被分配另一个从 到 的唯一值,称为种子,代表其在季后赛中的起始位置。
锦标赛由 场比赛组成。比赛方式如下:球队分成两对:种子队 对阵种子队 ,种子队 对阵种子队 (完全按照此顺序),并且依此类推(因此, 游戏在该阶段进行)。当一支球队输掉一场比赛时,该球队就会被淘汰。
之后,只剩下 队。如果只剩下一支球队,则宣布该球队为冠军;否则,将进行 场比赛:在第一场比赛中,“种子 vs 种子 ”游戏的获胜者与“种子 vs 种子 ”游戏的获胜者进行比赛,然后“种子 vs 种子 ”游戏的获胜者将与“种子 vs 种子 ”游戏的获胜者进行比赛,依此类推。重复此过程,直到只剩下一个团队。
比赛结束后,按照淘汰时的比赛阶段分配名额。尤其:
- 锦标赛获胜者获得名额 ;
- 决赛中被淘汰的球队获得名额 ;
- 半决赛中被淘汰的两支球队均获得席位 ;
- 所有在四分之一决赛中被淘汰的球队都获得席位 ;
- 所有在1/8决赛中被淘汰的球队都获得名额 ,以此类推。
既然我们制定了规则,我们就做一些操纵。我们特别希望:
- 队(不是种子队 )参加 ;
- 团队 进行 ;
- 队伍 和 进行 ;
- 从 到 的队伍将参加 ,依此类推。
例如,这张图片描述了锦标赛使用 进行的一种可能的方式,以及球队的最终名次:
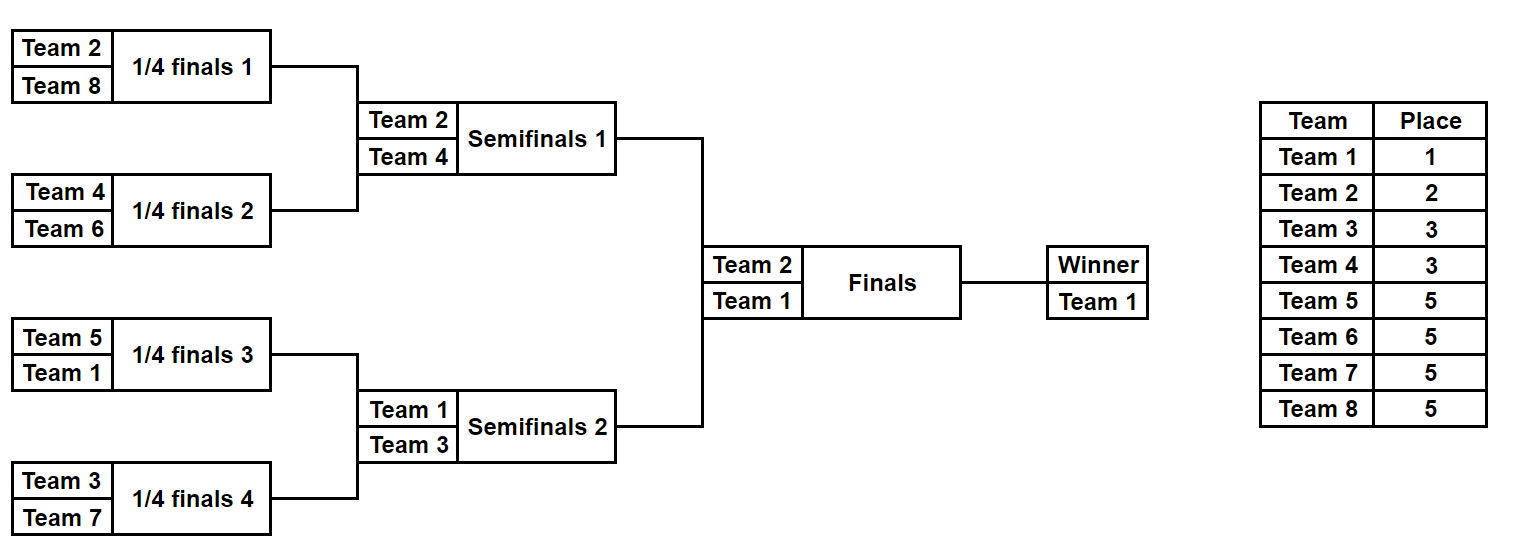
一些种子已经为一些球队保留了(显然,我们并不是唯一操纵锦标赛的球队)。我们必须用剩下的球队来填补剩下的种子,以达到预期的名次。有多少种方法可以做到这一点?由于该值可能很大,因此打印它对 取模。
Input
The first line contains a single integer $k$ ($0 \le k \le 19$) — there are $2^k$ teams.
The second line contains $2^k$ integers $a_1, a_2, \dots, a_{2^k}$ ($a_i = -1$ or $1 \le a_i \le 2^k$). If $a_i \ne -1$, then team $a_i$ has seed $i$. Otherwise, the seed $i$ is not reserved for any team.
All values, that are not $-1$, are distinct.
Output
Print a single integer — the number of ways to fill the non-reserved seeds so that the tournament goes as planned, modulo $998\,244\,353$.
2
1 2 3 4
2
1 3 4 2
1
-1 -1
2
-1 -1 -1 -1
3
-1 -1 -1 -1 2 -1 -1 -1
0
1
0
1
2
16
768
1
